轮换对称性有以下性质
下面来看一道例题
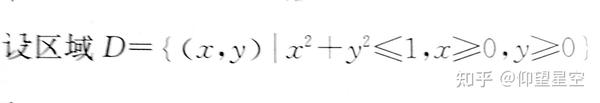
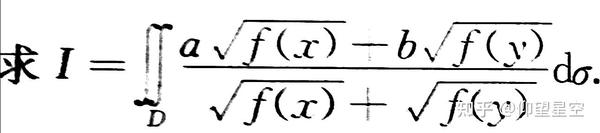
其中f(x)为D上连续函数，a、b均为常数
由轮换对称性
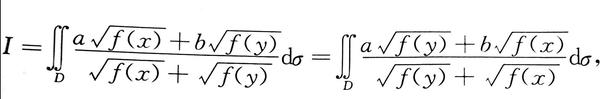
2I=∫∫(a+b)dσ
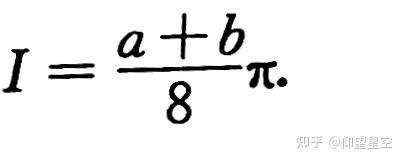
明显的，计算量得到了减少
与二重积分类似，调换x、y、z顺序积分区域不变，则三重积分同样满足轮换对称性
实际上，对任意多个变量的函数，只要满足
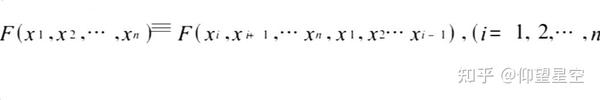
F就具有轮换对称性
例
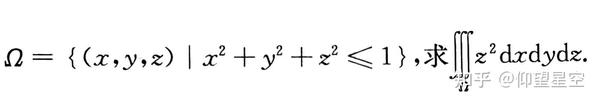
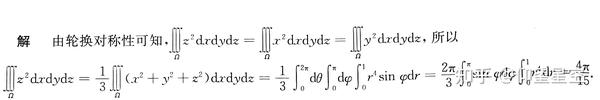
轮换对称性是积分中简化计算的重要方法，希望大家熟练掌握这一特殊性质，毕竟，数学的美感，许多时候不就体现于对称之中吗？
再看一道例题：
一个懒惰的程序员
一个懒惰的程序员
轮换对称性有以下性质
下面来看一道例题
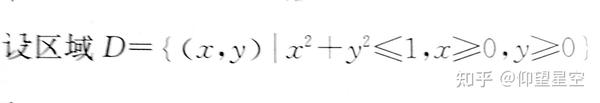
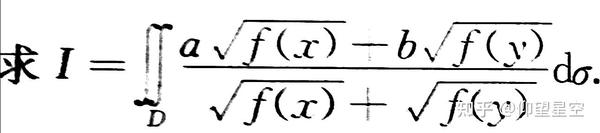
其中f(x)为D上连续函数，a、b均为常数
由轮换对称性
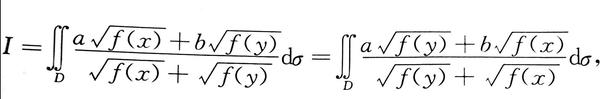
2I=∫∫(a+b)dσ
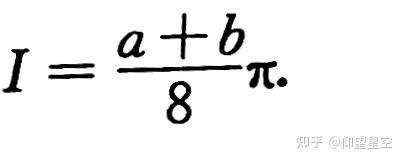
明显的，计算量得到了减少
与二重积分类似，调换x、y、z顺序积分区域不变，则三重积分同样满足轮换对称性
实际上，对任意多个变量的函数，只要满足
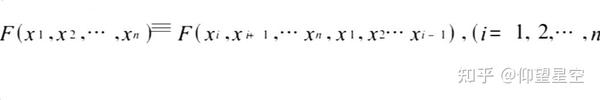
F就具有轮换对称性
例
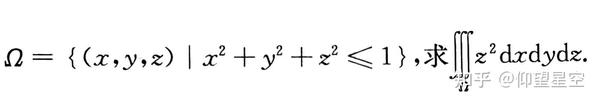
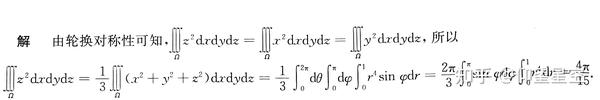
轮换对称性是积分中简化计算的重要方法，希望大家熟练掌握这一特殊性质，毕竟，数学的美感，许多时候不就体现于对称之中吗？
再看一道例题：